第2章整体结构

习题2

1. 证明：Feistel结构为对合结构，即加解密结构相同

上图为单轮 Feistel 结构的示意图。

加密： $Y_{0} = X_{1}, Y_{1} = X_{0} \oplus F_{K} (X_{1})$
解密： $X_{1} = Y_{0}, X_{0} = Y_{1} \oplus F_{K} (Y_{0})$

更“学术”的写法如下：
定义两个变换 $σ (L, R) = (R, L), τ_{K} (L, R) = (L \oplus F_{K} (R), R)$
显然 $σ^{- 1} = σ, τ_{K}^{- 1} = τ_{K}$ ，即 $σ$ 和 $τ_{K}$ 是对合变换
可将第 i 轮的变换表示为 $(L_{i}, R_{i}) = E_{K} (L_{i - 1}, R_{i - 1}) = (R_{i - 1}, F_{K} (R_{i - 1}) \oplus L_{i - 1}) = σ \circ τ_{K} (L_{i - 1}, R_{i - 1})$
则 $E_{K}^{- 1} (L_{i}, R_{i}) = (σ \circ τ_{K})^{- 1} = τ_{K}^{- 1} \circ σ^{- 1} = τ_{K} \circ σ = σ \circ τ_{K} = E_{K}$

结构完全一样啊！
我估计 Feistel 结构之所以设计成只加密一半，就是为了使得解密方便
（就好像给鞭炮留了一个引信，一点火就顺着往上炸完了）

2. 证明：当轮函数中 $F$ 函数可逆时，Feistel 结构存在5轮不可能差分区分器，并举例说明

这一问其实书里已经详细讲清楚了，我就沿用书里介绍的那个5轮不可能差分区分器了

顺便一提，差分区分器的本质就是看输入差分与输出差分的组合不可能是哪些组合

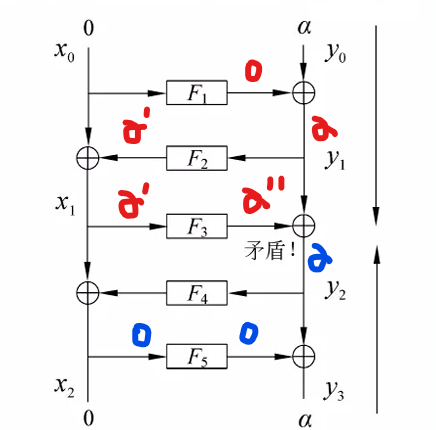
如上图，直接把这个不可能差分区分器告诉你，~~至于它是怎么得来的，我也不知道~~
假设输入差分是 $(0, α)$ ，输出差分是 $(0, α)$ ，那么 $(0, α) \to (0, α)$ 构成一个5轮的不可能差分区分器

分组密码中通常假设轮函数 $F$ 是随机置换函数（也就是双射函数）
因此，输入差分为0的一对数经过 $F$ 处理后，输出差分也是0（输入差分为0代表这两个数相等）
相应地，输出差分为0的一对数在经过 $F$ 前，输入差分也是0
若输入差分不为0，则输出差分是非0的某个数；输出差分不为0，则输入差分是非0的某个数

3. 若n轮 Feistel 结构输入差分为 $α$ ，输出差分仍为 $α$ ，则定义其为n轮循环差分。假设 Feistel 结构 $F$ 函数可逆，试证明其最多存在多少轮循环差分

假设该结构为 $L_{i} = R_{i - 1}, R_{i} = L_{i - 1} \oplus F_{i} (R_{i - 1})$
对于这种问题，我只能想到以下几种出发点：

输入差分为 $(α, α)$
$L_{0} = α, R_{0} = α$
$L_{1} = α, R_{1} = α \oplus F_{1} (α)$
$L_{2} = α \oplus F_{1} (α), R_{2} = α \oplus F_{2} (α \oplus F_{1} (α))$
……
没完没了了，肯定不行
输入差分为 $(α, 0)$
$L_{0} = α, R_{0} = 0$
$L_{1} = 0, R_{1} = α \oplus F_{1} (0) = α$
$L_{2} = α, R_{2} = 0 \oplus F_{2} (α) = F_{2} (α)$
$L_{3} = F_{2} (α), R_{3} = α \oplus F_{3} (F_{2} (α))$
……
也阵亡了
输入差分为 $(0, α)$
$L_{0} = 0, R_{0} = α$
$L_{1} = α, R_{1} = 0 \oplus F_{1} (α) = F_{1} (α)$
$L_{2} = F_{1} (α), R_{2} = α \oplus F_{2} (F_{1} (α))$
……
不过虽然没有循环差分，但是有不可能差分（参考第二题）

如上所示，我的这些尝试皆以失败告终，~~所以Feistel不存在循环差分~~

这时我看到题目里的这个要求： $F$ 可逆
顿时想到，可以设 $α = F^{- 1} (β)$
于是有了以下构造：
$L_{0} = α, R_{0} = β$
$L_{1} = β, R_{1} = α \oplus F_{1} (β)$
$L_{2} = α \oplus F_{1} (β), R_{2} = β \oplus F_{2} (α \oplus F_{1} (β))$
$L_{3} = β \oplus F_{2} (α \oplus F_{1} (β)), R_{3} = α \oplus F_{1} (β) \oplus F_{3} (β \oplus F_{2} (α \oplus F_{1} (β)))$
……

事实上，轮数最多的是3轮，但是要证明这一点，我暂时没想到什么很好的方法……

但其实，在实际研究差分攻击时，我们通常并不考虑找到一条百分百成立的差分特征
而是找高概率成立的就足够了

4. 为何Feistel结构中的 $F$ 函数不要求可逆？结合Feistel结构和SP结构，构造一个整体对合结构

因为解密的过程并不需要对F求逆。而SP结构中解密是需要求逆的（除非是对合SP结构）。

结合Feistel和SP结构的对合结构……这不就是简化版DES吗🤔

把DES里的8个不同S盒换成相同的S盒，相当于只是把F函数构造成SP结构，整体上还是对合的Feistel结构

习题2

1. 证明：Feistel结构为对合结构，即加解密结构相同

2. 证明：当轮函数中 F 函数可逆时，Feistel 结构存在5轮不可能差分区分器，并举例说明

3. 若n轮 Feistel 结构输入差分为α，输出差分仍为α，则定义其为n轮循环差分。假设 Feistel 结构F函数可逆，试证明其最多存在多少轮循环差分

4. 为何Feistel结构中的 F 函数不要求可逆？结合Feistel结构和SP结构，构造一个整体对合结构

2. 证明：当轮函数中 $F$ 函数可逆时，Feistel 结构存在5轮不可能差分区分器，并举例说明

3. 若n轮 Feistel 结构输入差分为 $α$ ，输出差分仍为 $α$ ，则定义其为n轮循环差分。假设 Feistel 结构 $F$ 函数可逆，试证明其最多存在多少轮循环差分

4. 为何Feistel结构中的 $F$ 函数不要求可逆？结合Feistel结构和SP结构，构造一个整体对合结构